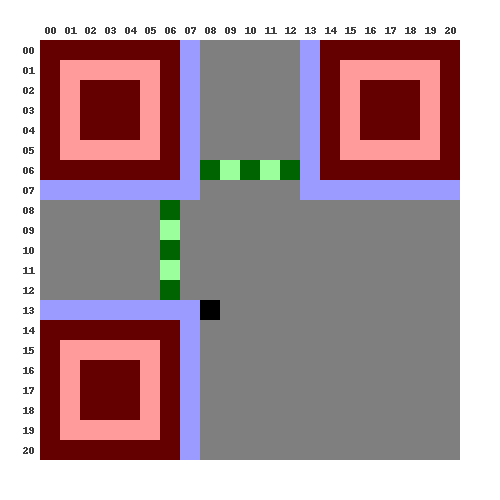
Pour cette première étape, le but à atteindre est l'affichage des modules fixes du QR-code. Dans le format QR-code version 1, que nous utilisons pour ce projet, certains modules sont toujours de la même couleur, peu importe le message encodé ou les autres paramètres du QR-code. On appelle donc ces modules des modules fixes. Les modules fixes sont présentés en couleur sur l'image suivante :

Parmi ces modules fixes, on a :
Sur les QR-codes que votre programme va générer, ces modules fixes ne seront bien entendu pas en couleur comme sur le schéma, mais en noir et blanc.

Pour cette première étape, nous vous fournissons tous les fichiers de base du projet. Ces fichiers sont à placer dans votre espace de travail.
Téléchargez l'archive du projet à l'adresse : qr.redelmann.ch/qr.zip, puis déplacez le dossier qr sur le Bureau.
Ouvrez ensuite le fichier qr.py depuis IDLE. Ce fichier contient le code à compléter dans cette première étape.
Dans cette étape, vous devez compléter la fonction placer_modules_fixes dont un squelette vous est donné. Le rôle de cette fonction est de placer les modules fixes du QR-code à générer tel que décrits plus haut. Vous pouvez bien entendu vous aider de fonctions annexes.
Pour dessiner un module, vous pouvez utiliser la fonction placer_module, qui place un module dans l'image donnée, aux coordonnées x et y données, en utilisant la couleur donnée.
Nous vous conseillons de procéder par type de schéma, en vous aidant de fonctions annexes. Des conseils pour vous aider sont disponibles ci-après.
Pour tester votre projet, il nous faudra exécuter le script generer-qr.py qui se trouve dans le dossier qr. Ouvrez ce fichier dans IDLE. Comme vous pouvez le voir en lisant le code, le fichier sert de point d'entrée au programme. Il sert à appeler les différentes fonctions que vous aller implémenter tout au long du projet et à les combiner en un unique programme.
Une fois le fichier generer-qr.py ouvert dans IDLE, exécutez-le via le menu Run > Run… Customized. Run… Customized permet d'ajouter des arguments à l'exécution de notre code.
Dans la boîte de texte qui apparaît au lancement, tappez le texte suivant : --etape 1
Vous pouvez même inscrire : --etape 1 --numeros pour afficher les numéros de ligne et de colonne autour du code QR.
Ensuite, cliquez sur OK pour lancer l'exécution.
Avant d'apporter vos changements, l'image obtenue devrait être la suivante :

Initialement, chaque module du QR-code est affiché en gris.
À la fin de l'étape, le résultat attendu est le suivant :

Alternativement, il est possible de lancer votre programme depuis le Terminal à la place de IDLE. Pour ce faire, ouvrez un nouveau terminal et déplacez-vous dans le dossier du projet via la commande suivante :
cd Desktop/qr/Il vous suffit ensuite simplement d'exécuter la commande suivante pour afficher le résultat de la première étape :
python3 generer-qr.py --etape 1Tester depuis le Terminal vous permet aussi de lancer une batterie de tests qui utilisent votre code et comparent les résultats obtenus à des résultats de référence. Pour cela, il suffit de tapper la commande suivante dans le Terminal :
python3 -m unittest test.Etape1Bon code !
Comme le schéma de positionnement est répété 3 fois, il est intéressant de concevoir une fonction qui affiche un tel schéma dans l'image. Cette fonction prendrait en argument l'image dans laquelle afficher le schéma, ainsi que les coordonnées x et y du module à l'extrémité supérieure gauche du schéma.
def placer_positionnement(img, x, y):
# Affichage d'un schéma de positionnement
passIl suffirait ensuite de faire appel à cette fonction à trois reprises dans la fonction placer_modules_fixes afin de placer ces schémas aux coordonnées désirées.
Pour le contenu même de la fonction placer_positionnement, il y a de nombreuses façons de procéder. Une façon assez simple consiste à dessiner un carré noir de dimension 7 par 7, puis, à l'intérieur de ce carré, de dessiner un carré blanc de dimension 5 par 5, et enfin, à l'intérieur de ce carré-ci, de dessiner un carré noir de dimension 3 par 3. Si vous décidez de procéder ainsi, il serait peut-être judicieux de prévoir une fonction placer_carre.
Pour les schéma d'espacement, il s'agit simplement de placer des segments horizontaux et verticaux dans les zones désirées. Pour ce faire, vous pouvez simplement utiliser une boucle par segment.
Une autre façon de procéder consiste à placer un carré blanc de dimension 8 par 8 dans les coins supérieurs et dans le coin inférieur gauche, puis de placer les schémas de positionnement par dessus. Si vous décidez de procéder ainsi, soyez sûr de placer ces carrés blancs avant de placer les schémas de positionnement.
Pour les schémas de cadencement, il s'agit simplement de placer deux segments de longueurs 5, de couleur alternant entre le noir et le blanc.
Si vous décider d'utiliser une boucle pour placer les modules de ces segments, nous vous conseillons d'utiliser une variable pour déterminer la couleur du module. À l'aide de l'opérateur binaire % (modulo, le reste de la division), il est possible de déterminer si l'itération courrante est paire ou impaire, et de choisir la couleur du module à placer en conséquence.
Pour placer le module noir, rien de magique, il suffit d'appeler la fonction placer_module avec les bons arguments.
Si vous avez terminé de placer les modules fixes du QR-code, vous avez fini le code demandé pour la journée. Bravo !
Si vous avez le temps, nous vous suggérons d'aborder l'exercice suivant, qui devrait vous aider à comprendre les notions abordées demain.
Pour cet exercice, vous allez concevoir une fonction pour calculer le reste d'une division entière. Comme on l'a vu aujourd'hui, cette opération est directement disponible en Python, via l'opérateur %. Cependant, il est possible d'implémenter cette opération à l'aide uniquement d'opérations simples comme la soustraction et la multiplication par deux. Procéder ainsi nous sera très utile demain, quand nous substituerons aux opérations arithmétiques traditionnelles d'autres opérations plus... intéressantes !
Pour travailler sur cet exercice, créez un nouveau fichier appelé reste_division.py hors du dossier qr, dans votre dossier d'exercices par exemple.
L'algorithme de calcul du reste de la division part des observations suivantes:
a par b (c'est-à-dire a % b) et que b est strictement plus grand que a, alors le reste est simplement a.a est plus grand ou égal à b, on peut soustraire b de a sans modifier le résultat.Ces deux observations combinées nous offrent une procédure pour calculer le reste de la division: Tant que a est plus grand ou égal à b, on retranche b de a. Enfin, on retourne a.
En vous basant sur cette description, implémentez la fonction suivante pour calculer a % b:
def reste_division_1(a, b):
passQue se passe-t'il lorsque b vaut 0 ? Ou 1 ?
Combien d'itérations sont effectuées pour le calcul des expressions suivantes ?
reste_division_1(4, 5)reste_division_1(54, 5)reste_division_1(504, 5)Bien que correcte, la procédure décrite plus haut est un peu lente en pratique: Le nombre d'itérations est fonction du facteur entre a et b, facteur qui peut être très grand en pratique.
Pour vous rendre compte du temps passé à calculer, vous pouvez essayer d'appeler votre fonction avec, par exemple:
reste_division_1(5000004, 5)reste_division_1(50000004, 5)reste_division_1(500000004, 5)Pour tester votre code de manière interactive, vous pouvez simplement vous contenter d'écrire vos fonctions dans votre fichier et les appeler depuis la console Python. Pour ce faire, une fois votre fonction définie, exécutez votre programme via Run > Run Module puis, dans le console qui s'ouvre, entrez du code, par exemple un des appels de fonctions inscrits plus haut. Aussi, vous pouvez utiliser ctrl-C dans la console pour forcer l'arrêt du calcul.
Pour calculer ce reste plus efficacement, nous allons nous baser sur l'observation suivante: On peut retrancher de a non seulement b, mais aussi n'importe quel multiple de b, tant que ce multiple n'est pas plus grand que a, et ce sans affecter la valeur a % b.
Les multiples de b que l'on va retrancher seront de la forme 2k · b. La première étape consiste à trouver le k le plus grand possible tel que 2k · b est toujours plus petit ou égal à a.
Pour cela, l'on peut s'aider d'une boucle.
La deuxième étape consiste à tester, pour chaque nombre i de k jusqu'à 1, si a est plus grand ou égal à 2i · b. Si c'est le cas, il est possible de retrancher 2i · b de a avant de passer à l'itération suivante.
Implémentez la fonction suivante à l'aide de la méthode décrite :
def reste_division_2(a, b):
# Première étape: trouver k
# Deuxième étape: retrancher les multiples de b.
passCette nouvelle implémentation est plus complexe que la précédente et compte plus de ligne de code. Cependant, comme on peut s'en assurer en testant son efficacé, la nouvelle fonction est beaucoup plus rapide que la précédente.
reste_division_2(5000004, 5)reste_division_2(50000004, 5)reste_division_2(500000004, 5)reste_division_2(50000000000000000000000000000000000004, 5)À partir de quel nombre avez-vous le sentiment de devoir attendre le résultat ?
Demain, lors du projet, nous continuerons à définir comment placer des modules sur le QR-code à générer. Cependant, contrairement aux modules placés aujourd'hui, il ne s'agira pas de modules fixes. Il nous faudra calculer la couleur des modules en fonction de divers paramètres.
Nous utiliserons aussi un premier code correcteur d'erreurs, ce qui rendra la lecture du QR-code résiliente à des modifications (par exemple dues à des saletés). Ce code correcteur d'erreurs utilisera une procédure très proche de celle du calcul du reste de la division tel que vous l'avez travaillé aujourd'hui !