Dans cette deuxième étape, nous allons nous occuper des modules de format des QR-codes générés. Les modules de format indiquent deux paramètres du QR-code:
Sans ces informations, il est impossible de lire le contenu encodé dans le QR-code. C'est pourquoi il est important que ces données soient transmises de manière fiable. Sur les QR-codes, ces informations sont encodées à l'aide d'un code correcteur d'erreur appelé code BCH(15, 5).
Dans cette étape, nous allons donc non seulement placer les modules qui correspondent au format dans le QR-code, mais aussi calculer leur valeur (couleur noire ou blanche) à l'aide d'un code correcteur !
Afin de faciliter votre travail, nous vous suggérons de commencer par définir la logique de placement des bits du format, et ce avant de les calculer.
Commencez par ajouter le code suivant à la fin du fichier qr.py dans le dossier de votre projet :
def bit(n, i):
return (n >> i) & 1
def couleur_module(b):
if b == 1:
return NOIR
return BLANC
def placer_modules_format(img, format_encode):
# À compléter.
passLa fonction bit permet de retourner le nième bit depuis la droite dans le nombre passé en argument.
La fonction couleur_module retourne la couleur d'un module en fonction de la valeur du bit à afficher: noir pour un bit à 1, blanc pour un bit à 0.
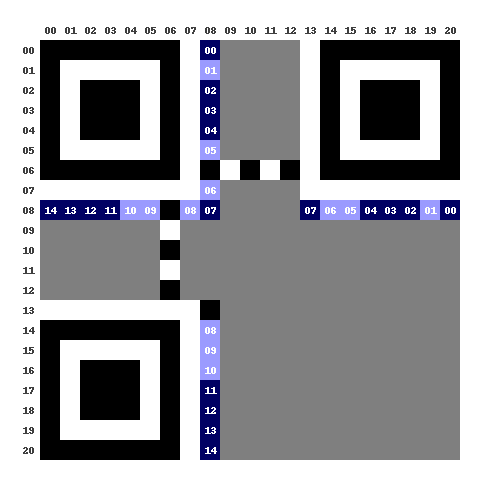
La fonction placer_modules_format, qui est à compléter, doit placer les bits qui correspondent au format. L'argument format_encode est un nombre entier, dont les bits représentent les données encodées du format. Ces bits doivent être placés dans le QR-code sur les positions indiquées en bleu. Le numéro inscrit dans chacun de ces modules indique le numéro du bit correspondant. À noter que chaque bit est affiché deux fois !

Le code correcteur d'erreur utilisé pour encoder les données du format fait usage d'une opération que nous avons abordé ce matin: le reste de la division de polynômes avec coefficients binaires (c'est-à-dire 0 et 1). Nous allons donc commencer par implémenter cette fonction, que nous allons appeler modulo.
Le squelette de la fonction, qui se trouve dans le fichier galois.py, est le suivant:
def modulo(dividende, diviseur):
passDans le fichier, vous trouverez aussi la fonction degre qui retourne le degré du polynôme passé en argument, ou -1 pour 0.
def degre(n):
d = -1
while n > 0:
n = n >> 1
d += 1
return dPour rappel, il est possible de considérer un nombre entier comme un polynôme à coefficients binaires.
En effet, chaque nombre nombre, par exemple 18, correspond à une séquence de bits, ici 10010.
Cette séquence de bits peut être interprétée comme un polynôme, ici 1x4 + 0x3 + 0x2 + 1x1 + 0x0, c'est-à-dire x4 + x.
Pour additionner deux tels polynômes, il suffit d'additionner les coefficients qui correspondent au même degré, et ce de façon indépendante pour chaque degré. Par exemple, si l'on additionne le polynôme x3 + x2 et le polynôme x2 + x1, on obtient comme résultat le polynôme x3 + x1. Comme on utilise l'arithmétique modulaire en mod 2, on a que 1 + 1 = 0; les coefficients de x2 s'annulent dans cet exemple.
En python, cette addition de polynômes à coefficients binaires existe de base dans le langage: il s'agit de l'opérateur binaire ^, appelé ou-exclusif.
De plus, en arithmétique modulaire mod 2, l'addition est exactement la même opération que la soustraction.
En Python, pour soustraire un polynôme à coefficients binaires encodé à l'aide d'un entier n1 d'un autre tel polynôme n2, il suffit donc d'écrire n1 ^ n2.
À noter qu'il est aussi très facile de multiplier un polynôme à coefficients binaires p par un polynôme xd. Pour cela, on peut utiliser l'opérateur << (appelé décalage à gauche, ou left-shift en anglais). La valeur p << d représente donc le polynôme p · xd.
Calculer le reste de la division d'un polynôme à coefficients binaires par un autre tel polynôme est au final assez simple.
Tout d'abord, observons que si le degré du dividende est strictement plus petit que celui du diviseur, alors il n'y a rien à faire, le reste est tout simplement le dividende.
Autrement, quand le degré du dividende (que l'on appelera d1) est plus grand ou égal à celui du diviseur (d2), on peut soustraire du dividende un polynôme qui est le produit du diviseur par le polynôme xd1-d2. Consultez la section de rappel au besoin pour trouver comment effecter facilement de telles opérations en Python.
Par exemple, considérons le dividende x6 + x3 + x2 + x0 et le diviseur x3 + x1 + x0. Le dégré du dividende (6) étant plus grand ou égal à celui du diviseur (3), il est possible de soustraire du dividende le produit du diviseur par x6-3 (c'est-à-dire x3). C'est ce qui est montré en dessous:
Bits Polynômes 1 0 0 1 1 0 1 x6 + x3 + x2 + x0 - 1 0 1 1 . . . x6 + x4 + x3 (= (x3 + x1 + x0) · x3) = 0 0 1 0 1 0 1 x4 + x2 + x0
Il est possible d'appliquer en boucle la procédure détaillée dans les précédents paragraphes tant que le degré du dividende est plus grand ou égal à celui du diviseur. À noter que chaque application de la procédure des précédents paragraphes baisse obligatoirement le degré du polynôme dividende, ce qui signifie que l'on ne risque pas de boucler pour toujours en appliquant cette opération en boucle. Dans l'exemple donné, l'itération suivante de la boucle effectue la soustraction suivante:
Bits Polynômes 1 0 1 0 1 x4 + x2 + x0 - 1 0 1 1 . x4 + x2 + x1 (= (x3 + x1 + x0) · x1) = 0 0 0 1 1 x1 + x0
À la fin de cette itération, le nouveau dividende (x1 + x0) est de degré strictement inférieur au degré du diviseur (x3 + x1 + x0), la boucle s'arrête donc à ce moment.
N'oubliez pas de retourner la valeur finale avec l'instruction return.
Une fois la fonction modulo implémentée, le travail pour cette étape est presque terminé ! Il nous reste simplement à implémenter la fonction encode_format.
def encode_format(mode, masque):
# À implémenter.
return 0Telle qu'elle est implémentée initialement, la fonction retourne toujours la même valeur, 0. Nous allons changer ça.
La fonction prend en entrée un numéro de mode (nombre de 0 à 3) et un numéro de masque (nombre de 0 à 7). Comme le nombre mode est entre 0 et 3, il peut être représenté fidélement sur 2 bits (M1 et M0), alors que le nombre masque doit occuper 3 bits (Q2, Q1 et Q0).
La première étape consiste à calculer un nombre dont la représentation binaire est donnée par:
M1 M0 Q2 Q1 Q0 0 0 0 0 0 0 0 0 0 0
Pour obtenir ce nombre, nous vous conseillons d'utiliser les opérateur << et ^.
Ce nombre est ensuite considéré comme le polynôme dividende d'une division par le polynôme p = x10 + x8 + x5 + x4 + x2 + x1 + x0 (autrement dit le nombre 0b10100110111 en Python, ou 1335 en base 10).
Pour calculer le reste de cette division, il est temps d'appeler la fonction moduloque vous avez préalablement réalisée !
Une fois ce reste obtenu, il doit être ajouté au dividende initial, afin d'obtenir un polynôme divisible par le diviseur p.
Finalement, afin d'éviter des problèmes à la lecture, le format QR spécifie que le résultat obtenu doit encore être masqué par la valeur 0b101010000010010. Pour appliquer ce masque, il suffit simplement d'utiliser le ou-exclusif, c'est-à-dire ^.
Une fois ce résultat calculé, il ne reste plus qu'à le retourner de la fonction.
Une fois votre code implémenté, vérifiez que vous obtenez le bon affichage pour les paramètres que nous allons utiliser (mode numéro 1 et masque numéro 3).
Pour ce faire, exécutez votre programme via le menu Run > Run… Customized et entrez le texte suivant : --etape 2
La sortie suivante devrait vous être affichée :
Format: 111100010011101Et l'image suivante vous être présentée :

Si vous obtenez une sortie différente, il peut s'agir soit d'une erreur de placement des modules, soit d'une erreur du calcul des bits de formats. Assurez-vous en premier que les bits de formats calculés correspondent à ce qui est attendu.
À la fin de cette seconde étape du projet, vous pouvez exécuter la commande suivante (depuis le dossier du projet, depuis le Terminal) pour vérifier si vous avez bien implémenté les fonctionnalités attendues :
python3 -m unittest test.Etape2