
Ressources pour les exercices:
Dans cet exercice, nous allons implémenter les notions de poids et de distance de Hamming abordées plus tôt dans la journée, ce qui nous permettra ensuite d'implémenter une procédure de correction d'erreurs simple pour les codes BCH. Nous utiliserons ensuite cette procédure pour décoder les informations de format d'un QR code.
Le poids de Hamming d'une séquence de bits est défini comme le nombre de bits à 1 dans la séquence.
Le but ici est d'implémenter une fonction que vous appellerez poids_hamming et qui prends en argument un nombre entier et retourne le nombre de bits à 1 dans la représentation binaire du nombre.
Indice : Utilisez les opérations en Python qui agissent sur les bits de la représentation binaire du nombre.
Indice : Aidez-vous d'une boucle pour compter le nombre de bits à 1 en partant de la droite de la séquence de bits.
La distance de Hamming entre deux séquences de bits est définie comme le nombre de positions auxquelles les séquences diffèrent.
Votre but ici est d'implémenter une fonction, que vous appellerez distance_hamming, qui prends en argument deux nombres entiers et retourne la distance de Hamming entre ces deux nombres.
Indice : Il est possible d'implémenter cette fonction très facilement en faisant appel à la fonction précédente (poids_hamming) et à une opération bit-à-bit entre les deux nombres.
Considérez la liste de mots de codes mots définie comme suit:
mots = [
0b000000000000000,
0b000010100110111,
0b000101001101110,
0b000111101011001,
0b001000111101011,
0b001010011011100,
0b001101110000101,
0b001111010110010,
0b010001111010110,
0b010011011100001,
0b010100110111000,
0b010110010001111,
0b011001000111101,
0b011011100001010,
0b011100001010011,
0b011110101100100,
0b100001010011011,
0b100011110101100,
0b100100011110101,
0b100110111000010,
0b101001101110000,
0b101011001000111,
0b101100100011110,
0b101110000101001,
0b110000101001101,
0b110010001111010,
0b110101100100011,
0b110111000010100,
0b111000010100110,
0b111010110010001,
0b111101011001000,
0b111111111111111,
]Cette liste de mot correspond au code BCH(15, 5) vu plus tôt dans la journée.
Dans le cadre des QR codes, ces mots correspondent aux différents formats de QR codes. Pour chaque nombre, les deux bits les plus à gauche indiquent le mode de correction d'erreur (0 = Medium, 1 = Low, 2 = High, 3 = Quartile) et les trois bits suivant le masque appliqué (entre 0 et 7).
À l'aide de Python, trouvez la distance de Hamming la plus petite entre deux mots de code distincts dans mots.
Indice : Utilisez une boucle imbriquée dans une autre boucle.
Question de compréhension : Étant donné la distance trouvée, combien d'erreurs de bits peuvent être corrigées à l'aide de ce code ?
Écrivez une fonction appelée trouve_mot qui prend en argument un nombre entier et qui retourne le mot de code le plus proche (au sens de Hamming) de ce nombre.
Indice : Utilisez une boucle pour parcourir tous les mots de code et sélectionner le plus proche.
Nous allons maintenant pouvoir utiliser cette fonction de décodage pour lire le format d'un QR code. Considérez le QR-code suivant :

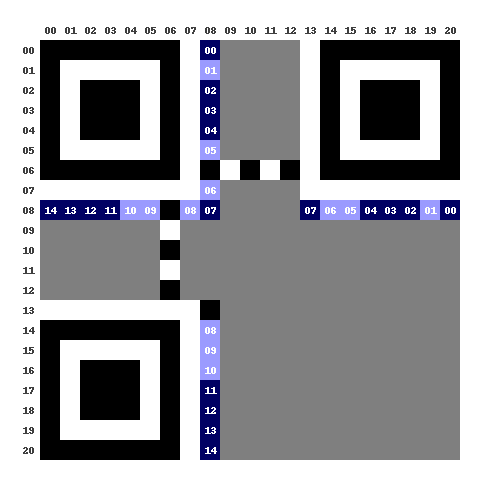
Les modules qui indiquent le format d'un QR code se trouvent autour des schémas de positionnement. Le schéma suivant indique leur position en bleu (ici avec une autre suite de bits de format). L'index 00 indique le bit le plus à droite, alors que l'index 14 indique le bit le plus à gauche de la séquence de bits.
Dans un premier temps, entrez dans une variable Python la valeur contenue dans les modules de format du premier QR code. Pour cela, il suffit simplement de lire et de reporter la valeur à la main.
Ensuite, appliquez un ou-exclusif avec le nombre 0b101010000010010.
Cette opération, qui est spécifiée dans le standard pour les QR codes, est mise en place afin d'éviter que les modules de format soient tous blancs ou tous noirs à l'affichage du QR code.
Finalement, utiliser votre fonction trouve_mot pour trouver le mot de code correspondant.
Questions : Quel est le mode de correction d'erreur utilisé par ce QR code ? Quel est le masque appliqué ? Y a-t-il eu des erreurs dans les bits de format, et si oui, en quelle(s) position(s) ?
Pour ce deuxième exercice, nous allons nous intéresser à la stéganographie, une discipline dont l'enjeu consiste à cacher discrètement des messages à l'intérieur d'autres messages, le but étant de pouvoir communiquer un message sensible sans éveiller de soupçons chez de potentiels observateurs.
Ce domaine est orthogonal à celui de la cryptographie, une discipline qui cherche à rendre incompréhensibles les messages pour toutes autres personnes que le destinaire prévu du message.
Pour cette première partie exercice, vous allez travailler sur une petite image de chat somme toute assez anodine :

Le créateur de l'image a cependant caché un message à l'intérieur de cette image. En effet, sous l'image de chat se cache une image en noir à blanc de même dimension. Pour cacher cette image en noir et blanc, le créateur de l'image a utilisé le bit de poids le plus faible (le plus à droite) de l'intensité de la couleur rouge de chaque pixel.
À l'aide de Python et de la libraire Pillow, ouvrez l'image de chat et reconstituez l'image cachée. Décodez ensuite le message, en vous aidant par exemple de votre téléphone.
Indice : N'hésitez pas à vous référer à la documentation de la classe Image de la librairie Pillow pour trouver comment ouvrir une image depuis un fichier, par exemple.
Indice : Utilisez une opération sur les bits du nombre qui indique l'intensité du rouge pour trouver la couleur du pixel de l'image caché.
Pour la seconde partie, le but est de concevoir :
Vous êtes libre de choisir la façon dont vous altérez l'image. Le but du jeu ici est de faire en sorte que les modifications apportées à l'image soient le plus discrètes possible. Évitez donc de modifier des bits avec un grand impact sur l'image.
L'information à cacher est une date, avec une précision à la minute. Pour ce faire, vous devez pouvoir cacher dans l'image les données suivantes :